Depuis le début du 20ème siècle les mathématiciens se sont rendu compte que les formules logiques qu’ils emploient ressemblent à des molécules. Elles s’agrègent les unes aux autres par des connecteurs logiques et peuvent se disloquer par les règles de déduction. Cette analogie forte entre la chimie et les systèmes formels axiomatisés ne doit pas faire oublier des différences évidentes entre les deux situations — température, énergie, valence, vitesse de réaction, etc. n’ont pas leur correspondant en mathématiques. Mais il n’y a pas d’obstacle néanmoins à s’en servir comme support d’une réflexion philosophique si l’on reste vigilent à n’en tirer que des interrogations ou des heuristiques qui concernent la combinatoire uniquement.
Il revient à Quine d’avoir montré la fécondité de cette façon de raisonner en philosophie lorsqu’il utilise des propriétés des langages formels pour mettre en évidence des phénomènes relatifs aux langues réelles, ce qui lui fit découvrir ses fameuses thèses de la relativité de l’ontologie, de l’indétermination de la traduction, et de la sous-détermination des théories par l’expérience. Les mathématiques sont alors utilisées selon une démarche que l’on peut appeler abductive où un modèle n’est pas destiné à résumer le réel ou en exprimer une loi mais plutôt à illustrer des possibilités de configurations compatibles avec ce qu’on sait et difficiles à imaginer.
Ce que les systèmes formels nous enseignent particulièrement clairement c’est la complexité des résultats des opérations de concaténation et de scission. L’itération de l’opération de coller ensemble puis de casser autrement n’est pas du tout quelque chose de simple. Même avec un petit nombre de formules finies au départ, le résultat peut être indécidable, c’est-à-dire être au-delà de ce que peuvent traiter les algorithmes.
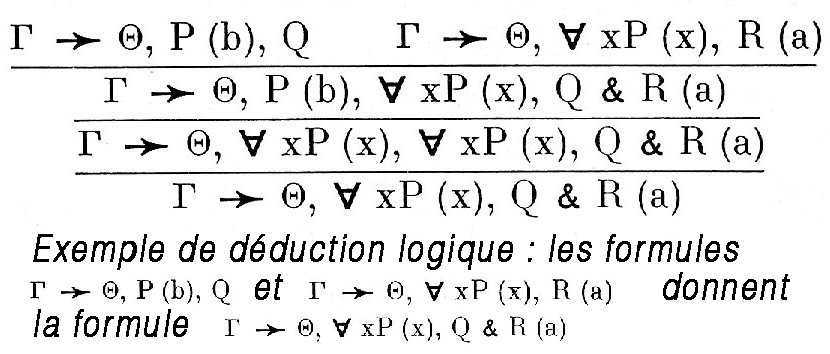Ceci porte à penser que la considération d’une protéine ne permet pas, en général, de savoir de quelle configuration génétique elle provient. Aussi les biologistes procèdent-ils dans l’autre sens, en perturbant le système génétique par addition d’une séquence provenant d’ailleurs pour voir ce qui se passe chez l’être vivant ainsi modifié.
La question qui se pose alors est double. D’une part savoir si le système modifié est viable — ce qui s’exprime en mathématique par le fait qu’il est non-contradictoire. D’autre part savoir si le système modifié est susceptible de perturber son environnement et de quelle façon. Et là l’analogie avec les mathématiques doit être raffinée en nous plaçant dans une sous-théorie d’une théorie donnée afin de disposer d’un contexte.
Dans cet esprit nous poussons la réflexion pour dégager des non-dits des pratiques de biologie de synthèse et des OGM.
Notre analyse conclut à la nature religieuse de la croyance des chercheurs à une résilience globale de la nature aux perturbations de la combinatoire génétique moléculaire.