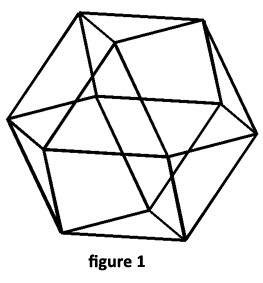
On se donne trois polygones plans réguliers de six cotés au plus, et de côtés de même longueur a. On en réunit deux par un côté puis le troisième aux deux précédents de sorte qu’on a nos trois polygones avec un sommet commun et tous les sommets sur une même sphère.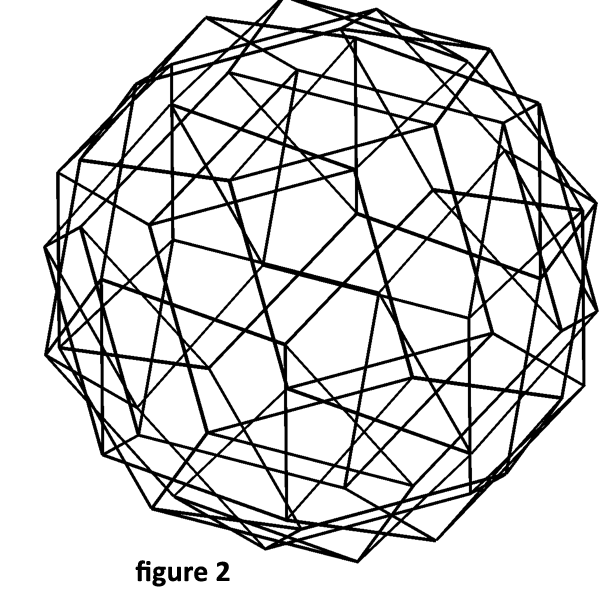 
Le procédé permet de continuer cet assemblage et on a toujours ainsi le début d’un polyèdre fermé dont les sommets sont reliés par des segments de longueur a mais ne dessinant pas forcément l’enveloppe convexe de ce polyèdre, les polygones initiaux n’étant pas forcément les faces extérieures du polyèdre. Par exemple avec 3, 4, 6, on obtient le polyèdre de la figure 1 (huitième polyèdre semi-régulier d’Archimède). Avec 4, 5, 6 on obtient le polyèdre de la figure 2, etc.
Que se passe-t-il si on dépasse six en prenant 5, 6, 7 ? C’est-à-dire en partant de :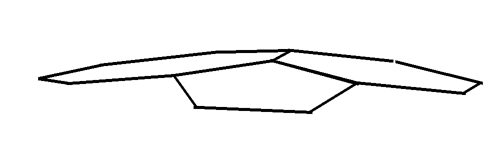
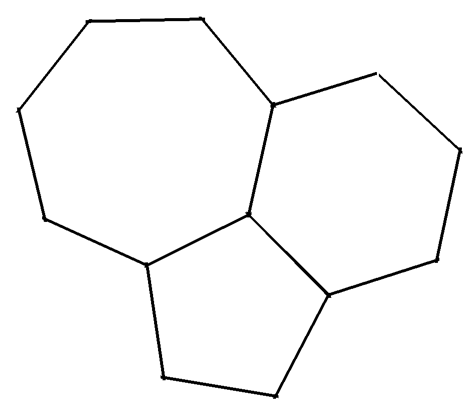
Les sommets sont sur une même sphère, les normales aux centres des polygones se coupent au centre de la sphère. On peut prolonger en ajoutant un pentagone entre l’hexagone et l’heptagone, etc.
On progresse ainsi vers un recouvrement de la sphère, seulement les coïncidences saturées au bout d’un nombre fini d’extensions ne se produisent plus.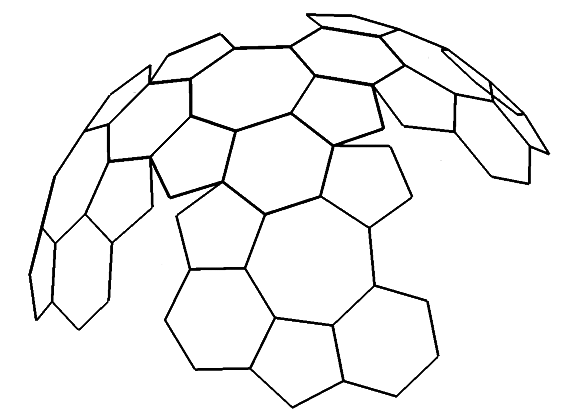 
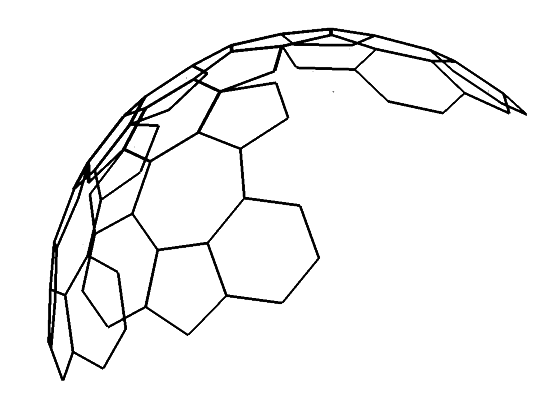
Par exemple si on considère un heptagone, on peut l’entourer d’une alternance de pentagones et d’hexagones, et comme 7 est impair, il faudra faire deux tours pour arriver à stabilisation. On a ainsi un heptagone avec une « jupe à deux volants » de pentagones et d’hexagones. Mais la figure n’est pas saturée. On peut montrer qu’il est impossible que l’on parvienne à un polyèdre fini où la suite du procédé ne donnerait rien de nouveau. C’est dû à ce que les sous-groupes finis de SO(3) sont connus pour correspondre 1°) soit aux rotations de 2kπ/n qui conservent un polygone régulier de n côtés, 2°) soit les mêmes avec les symétries qui conservent le même polygone 3°) soit correspondent au tétraèdre, 4°) soit au cube (ou octaèdre) 5°) soit au dodécaèdre (ou icosaèdre). Il n’y a pas de sous-groupe fini des rotations de R3 qui contienne les trois rotations de 2π/5, 2π/6, 2π/7, qui conservent chacun de nos trois polygones initiaux.
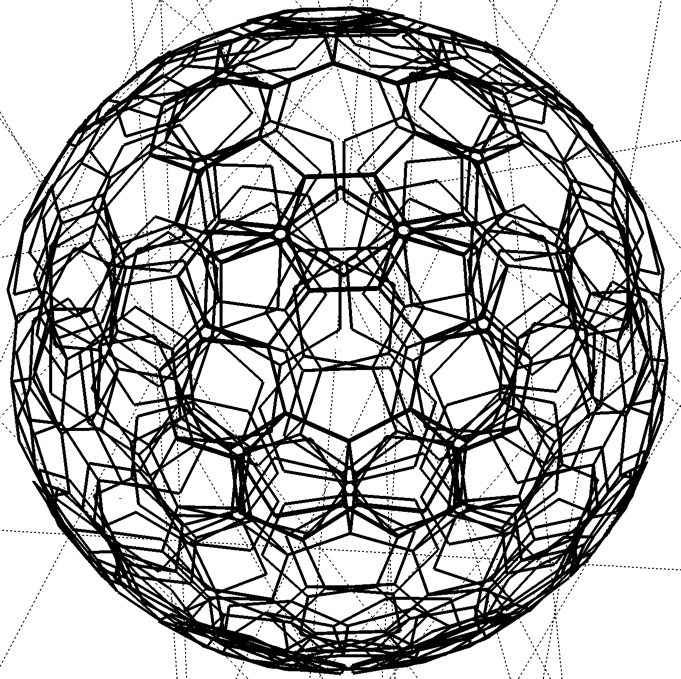Appelons « procédé » une suite infinie d’insertion de l’un de nos trois polygones selon la méthode ci-dessus, et « procédé contigu » une telle suite d’insertion où le suivant touche le précédent. Avec des notations évidentes un procédé contigu définit une suite de chiffres de la forme
5676576767565…
Mais toutes les suites formées des chiffres 5,6,7, ne conviennent pas, il n’y a pas deux fois le même chiffre à la suite puisque les pentagones ne se touchent pas, ni les hexagones ni les heptagones. En revanche une suite de chiffres 5,6,7 ne peut correspondre qu’à un seul procédé contigu.
Il y a des procédés contigus qui deviennent périodiques au bout d’un certain temps, comme on le voit à cause des « jupes » autour des <7> et des <5>. Ils sont ce qu’on peut appeler les procédés contigus rationnels. Leurs suites de chiffres sont les décimales d’un rationnel. En revanche si une suite de chiffres 5,6,7 est périodique elle ne correspond pas forcément à une suite périodique sur la sphère. Par exemple je conjecture que la suite 567567567567567567… définit, par les axes de polygones, une suite de points dense sur la sphère.
Il y a aussi des procédés contigus irrationnels dont les suites de chiffres sont les décimales de nombres irrationnels. Il y en a une infinité non dénombrable. Appelons « pivots » les points intersection des axes des polygones avec la sphère. Un procédé contigu irrationnel définit une infinité de pivots distincts.
Selon toute vraisemblance certains procédés contigus irrationnels ont une suite de pivots dense. Si, comme conjecturé ci-dessus, la suite qui répète 567 indéfiniment a une suite de pivots dense, tel est le cas également de toute suite irrationnelle qui contient des séquences de n fois 567 pour n aussi grand qu’on veut.
Je pense qu’il y a des procédés contigus irrationnels dont tous les pivots sont dans une demi-sphère donc ne forment pas un ensemble dense.
Considérons un procédé contigu irrationnel construit de sorte que dans les choix les pivots soient le plus proche possible d’un point de la sphère disons du pôle Nord. L’ensemble adhérence des pivots obtenus a-t-il un intérieur non vide ? Est-il possible que les pivots d’un procédé contigu irrationnel n’aient qu’un seul point d’accumulation ?