Lagrange, Joseph Louis Théorie des fonctions analytiques, contenant les principes du calcul différentiel, 3ème éd. revue et suivie d’une note par J.-A. Serret, Paris Bachelier 1847.
C’est en 1797 que paraît la première édition de la Théorie des fonctions analytiques de Lagrange. Je m’intéresse ici à la façon de s’exprimer de Lagrange et comment il parle des fonctions.
L’ouvrage débute ainsi : « Nous désignerons, en général, par la caractéristique f ou F, placée devant une variable, toute fonction de cette variable, c’est à dire toute quantité dépendante de cette variable et qui varie avec elle selon une loi donnée. »
Je relève que pour introduire la notion de fonction il se sert du terme de loi, alors qu’un peu plus tard Auguste Comte définira la loi scientifique comme ce qui est donné par une fonction mathématique.
En fait Lagrange veut rapidement arriver aux choses intéressantes et applique visiblement la philosophie pascalienne que chercher à tout définir apporterait plus d’obscurité que de lumière. Dès la seconde page, après quelques indications de pure notation, il est déjà à même de démontrer quelque chose : « Je vais d’abord démontrer que, dans la série résultante du développement de la fonction f(x+h), il ne peut se trouver de puissances fractionnaires de h, à moins qu’on ne donne à x des valeurs particulières. »
Le développement en question est le développement limité à un ordre quelconque non spécifié, la fonction est implicitement supposée suffisamment dérivable. Mais l’argument de la démonstration est assez extraordinaire : « si le développement de la fonction f(x+h) pouvait contenir un terme de la forme u hm/n, la fonction f(x) serait nécessairement irrationnelle, et aurait, par conséquent, un certain nombre de valeurs différentes qui serait le même pour la fonction f(x+h), ainsi que pour son développement. Mais ce développement étant représenté par la série f(x) + ph + qh2 + … + uhm/n + … chaque valeur de f(x) se combinerait avec chacune des n valeurs du radical 
; de sorte que la fonction f(x+h) développée aurait plus de valeurs différentes que la même fonction non développée, ce qui est absurde. »
Autrement dit si par exemple la fonction 
qui a trois valeurs, admettait dans le développement de 
des termes avec des racines n-ièmes de h, cela ferait 3n valeurs au lieu de 3. Dans cet exemple le développement est
Lagrange pense d’emblée avec des nombres complexes et il a présent à l’esprit le nombre de valeurs que prend une fonction lorsqu’on permute les racines de l’unité qui y interviennent, comme dans son fameux mémoire sur la résolution des équations algébriques de 1770. Il le disait dans une lettre à un collègue italien « Je regarde comme un des pas les plus importants que l’analyse ait faits ces derniers temps, de n’être plus embarrassée des quantités imaginaires et de pouvoir les soumettre au calcul comme des quantités réelles »[0]. Mais il n’est pas assez précis sur les hypothèses, nous ne voyons plus aujourd’hui clairement dans quel champ expressif se place ce grand mathématicien. Que recouvre exactement le concept de fonction dans l’esprit de Lagrange ? On voit qu’il a dans l’idée des fonctions qui font sens avec des arguments complexes, qui se définissent naturellement sur une partie du corps des complexes.
Certes comme on l’a souvent dit, au 18ème siècle jusqu’à Euler au moins, la notion de fonction n’est pas dissociée d’une référence à une expression formelle dans un certain vocabulaire.
Observons que ce champ expressif particulier a été précisé progressivement au cours du 19ème siècle, jusqu’à une rigueur parfaite bien avant que les mathématiques soient formalisées. Voici comment Henri Poincaré décrit ces travaux :
« La théorie moderne des fonctions analytiques a eu quatre fondateurs, Gauss, Cauchy, Riemann et Weierstrass.
Gauss n’a rien publié de son vivant […] les trois autres géomètres qui ont contribué à créer la notion nouvelle de fonction ont suivi des voies bien différentes.
Cauchy a précédé les deux autres et leur a montré le chemin. […] Pour Cauchy la définition de la fonction conserve encore un peu de l’indécision qu’elle avait chez ses devanciers. Il impose seulement aux fonctions analytiques quelques conditions restrictives comme celle d’avoir une dérivée continue. Tout repose sur un théorème très simple relatif aux intégrales imaginaires et sur la notion de résidu. […] La théorie de Cauchy contenait en germe à la fois la conception géométrique de Riemann et la conception arithmétique de Weierstrass […]
Pour Riemann, l’image géométrique joue un rôle dominant […] Weierstrass se place à l’extrême opposé; le point de départ est la série de puissances, l’élément de la fonction qui est confiné dans un cercle de convergence; pour poursuivre la fonction en dehors de ce cercle nous avons le procédé de prolongement analytique […] Nous sommes débarrassés des doutes, qui au siècle dernier, et dans la première moitié de ce siècle, assaillaient souvent les penseurs à propos des principes du calcul infinitésimal et aussi de ceux que pouvaient provoquer par ses lacunes la théorie des fonctions analytiques de Lagrange […] » (Henri Poincaré « L’œuvre mathématique de Weierstrass », Acta Mathematica 22, 1-18, (1899)).
On dit souvent que tout au long du 19ème siècle les mathématiciens ont pris en considération des fonctions de plus en plus générales, non dérivables, discontinues, etc., et on cite volontiers le mathématicien Bernard Bolzano (1781-1848), prêtre et théologien, qui, parmi des recherches abstraites et de tournure très moderne, construisit par itération une fonction continue non dérivable, de variation quadratique finie non nulle.
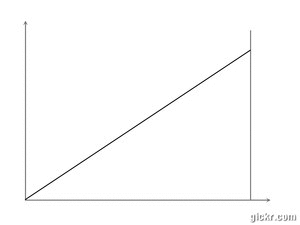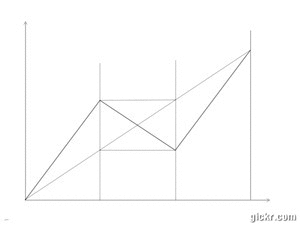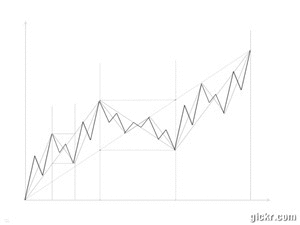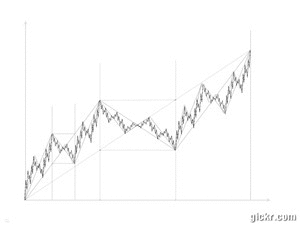
la fonction de Bolzano[1]
Mais peut-on suivre les auteurs (comme Jaroslav Folta[2]) qui écrivent que « Bolzano rejette l’identification eulérienne d’une fonction avec son expression analytique, introduisant la notion de fonction en termes de correspondance mutuelle de valeurs de deux ensembles » ? On peut les suivre si on se place d’un point de vue purement philosophique. Parce que, à cette époque on n’a pas de définition mathématique claire de la notion d’ensemble. Pour l’ensemble de départ, cela n’est pas dirimant, mais si on considère des fonctions compliquées la description des points atteints par la fonction fait intervenir des difficultés logiques qui ne seront élucidées que dans les années 1930.
Il reste que, si nous adoptons en effet ce point de vue philosophique attribué à Bolzano, en nous plaçant dans l’esprit du 19ème siècle, et en considérant que les fonctions mathématiques sont toutes les fonctions possibles et imaginables sans que tout ceci soit formalisé a priori, que devient alors le contenu réel de la thèse fondamentale du positivisme que la science consiste à dégager des lois qui s’expriment par des fonctions mathématiques ? Il me paraît évident qu’Auguste Comte, grand admirateur de Lagrange, pense comme ce dernier dans un champ expressif restreint qui seul peut donner une certaine valeur à la découverte d’une loi.
Découvrir ou proposer une loi d’expression très compliquée est moins convaincant parce qu’elle semble ad hoc. Ceci est merveilleusement discuté par Augustin Cournot lorsqu’il introduit le concept de « probabilité philosophiques » à la fin de son traité Exposition de la théorie des chances et des probabilités (1843), Œuvres complètes t1, Vrin 1984, je l’évoque au chapitre II de Risk and Meaning Springer 2011.
Ceci vaut pour les lois au sens de Comte mais aussi pour les lois au sens de Montesquieu. Par exemple l’ingénieur Caquot proposa en 1949 une formule pour le dimensionnement et la pente des égouts urbains qui fut longtemps utilisée et est restée justement célèbre pour son positivisme sans faux semblant.
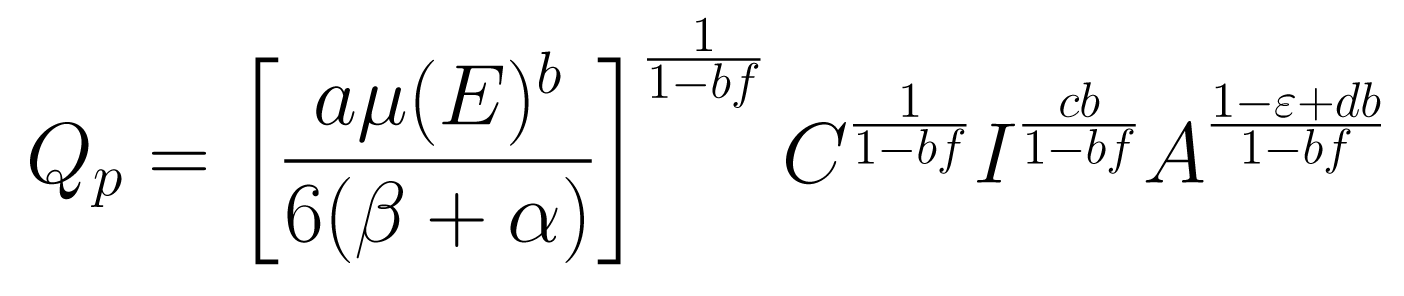
formule de Caquot
(voir http://www.scribd.com/doc/42191617/caquot♯outer page 5 , pour l’explication des lettres).
Si on accepte les formulations les plus générales, le problème d’ailleurs n’est pas seulement la question du mérite du découvreur. Il y a aussi la difficulté du nom, de la désignation précise, du moyen concret de reconnaître ce qui a été découvert.
Car, si un physicien dit qu’il y a une régularité dans telle circonstance mais est incapable de formuler la loi, on perd le moyen de dire dans quel cas on se trouvera dans les mêmes circonstances et pour vérifier l’exactitude du résultat physique on sera contraint de refaire l’expérience à l’identique – si cela n’est pas impossible –, car la loi se trouvera donnée par l’expérience elle-même uniquement.
Dans la référence à une loi mathématique chez Comte, il y a l’idée d’un moyen mnémotechnique, d’un dispositif capable de reproduire la régularité observée. Si on ne sait que l’observer, ce constat ne constitue pas en lui-même une régularité, et refaire l’expérience est impossible si le temps, la date, joue un rôle.
Sautons un siècle. Aujourd’hui nous disposons du cadre nous permettant de définir une fonction comme une application d’un ensemble dans un autre, le terme même d’application se définissant comme une partie de l’ensemble produit ayant la propriété d’univocité. Tout cela s’écrit parfaitement dans le langage formalisé de la théorie des ensembles (langage des prédicats du premier ordre muni des axiomes convenables).
Aujourd’hui les mathématiques sont formalisées. Donc cela voudrait dire que nous avons atteint une situation philosophique satisfaisante où d’une part nous acceptons toutes les fonctions aussi biscornues soient-elles, et où d’autre part tout se dit dans un langage absolument précis, où chaque terme est formé d’un nombre fini de signes. Mais alors on est – mutatis mutandis – dans une situation analogue à celle de Lagrange avec un vocabulaire plus vaste certes mais limité et donc un champ expressif particulier. Donc on ne peut pas désigner toutes les fonctions. Où est l’erreur ?
En fait, nous ne sommes pas exactement dans la même situation que celle d’Euler et de Lagrange parce que le langage de la théorie des ensembles avec ses axiomes (notamment le schéma de remplacement) permet de désigner par un terme un objet défini par une limite convergente. C’est analogue et plus simple à voir pour les nombres que pour les fonctions.
Je renvoie pour la suite de cette discussion à la page de ce blog intitulée le contrat de sublimation.
[0] lettre du 20 décembre 1777 De Lagrange à Lorgna, Œuvres tome 14 Paris 1868.
[1] B. Bolzano, Functionenlehre (1833-41) [K. Rychlik, ed.] in Spisy B. Bolzano, Vol. 1 Prague 1930.
[2] J. Folta « Life and scientific endeavour of Bernard Bolzano » in V. Jarnik Bolzano and the foundations of mathematical analysis, Soc. of Czechoslovak Mathematicians and Physicists 1981.