Au sous-sol de la Sagrada Familia on peut admirer les maquettes que Gaudi avait faites pour étudier les formes naturelles soumises à la gravité. Il suspendait son projet à l’envers, bas en haut, des ficelles remplaçant les piliers et des petits sacs de sables simulant les masses. Dans cette architecture funiculaire et caténaire, la forme la plus fondamentale est la chaînette et la verticale est l’exception.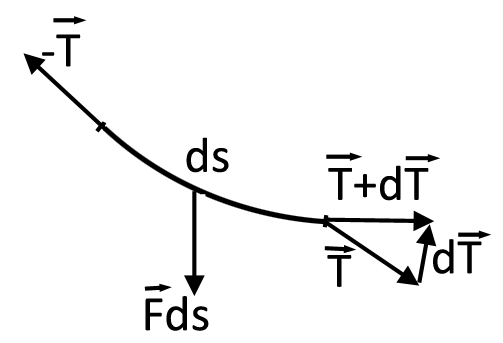
La mécanique des fils est un peu délicate et ne fut éclaircie, pour ce qui est de la statique, que vers la fin du 17e siècle sous l’impulsion de Jacques Bernoulli. J’en donne les principes dans les encarts. Les deux résultats les plus connus sont qu’un fil parfaitement flexible de densité linéaire constante prend sous son poids la forme d’un segment de chaînette [courbe d’équation y=(1/a) cosh ax] 
et que si c’est la projection horizontale du fil qui a une densité uniforme — comme c’est souvent le cas pour les ponts suspendus — alors la courbe est un segment de parabole.
La question qui se pose naturellement est de voir comment ces résultats s’étendent au cas des coupoles.
Considérons une coupole de révolution, de densité surfacique constante, retournée à la manière de Gaudi. Découpons-en une tranche entre deux méridiens voisins. Nous pouvons penser ce secteur comme un fil dont la densité n’est pas constante. Par les résultats sur la statique des fils nous avons le moyen d’étudier la courbe que prendrait ce fil sous son poids, et de comparer cette courbe avec celle du méridien.
Si la courbe spontanée du secteur est plus éloignée de l’axe de la coupole que le méridien, cela veut dire que la coupole a tendance à s’écarter, donc à se fissurer le long des méridiens. Si au contraire la courbe spontanée du secteur est plus proche de l’axe que le méridien cela signifie que la coupole est partout en compression.
Ces questions de compression ou traction sont fondamentales en architecture parce que les matériaux traditionnels — pierre, brique, ciment — « travaillent » bien en compression mais mal à la traction. D’où la révolution que furent la construction métallique et le béton armé.
Ceci étant, la courbe spontanée du secteur ne sera pas en général d’un seul côté de celle du méridien, il y aura des régions comprimées et des régions tendues. 
La surface « remarquable » qui joue un peu le rôle de chaînette pour les surfaces est celle qui serait telle que la courbe spontanée du secteur coïncide avec la forme du méridien. Une coupole de révolution de densité surfacique constante dont les méridiens ont cette forme, est telle que ses secteurs travaillent sans interaction entre eux, autrement dit, les sections horizontales que sont les parallèles ne sont ni comprimées ni tendues. La résolution mathématique de cette question n’est pas difficile (voir l’encart) simplement la courbe méridienne obtenue n’a pas un nom connu, elle a une équation de la forme
y=b∫0x sinh(cz2+d)dz.
Une telle coupole est plus plate qu’une sphère à son sommet (dans le cas d=0) et plus élancée dans sa silhouette générale (cf. figure). Elle n’a pas été utilisée en architecture à ma connaissance, quoique une telle coupole dans sa partie supérieure ressemble beaucoup à une sphère et justifie la stabilité des coupoles hémisphériques qui sont assez épaisses pour qu’on puisse tracer dans leur épaisseur cette coupole limite.
Bien des raisons historiques et méthodologiques font que l’architecture préfère les formes simples et leurs combinaisons. On peut en discuter à l’infini, évidemment. C’est l’opposition entre le classicisme et le baroque, ou plutôt entre l’architecture contrainte et composée et la vision fantaisiste et libertaire, entre disons le maître de Tournus, les cisterciens, Palladio, Ledoux, Le Corbusier, Louis Kahn, d’un côté et de l’autre Gaudi, le facteur Cheval, Frank Gehry. Je n’ouvre pas ici ce débat. D’un point de vue historique en tout cas c’est ainsi, la coupole sphérique fut la plus utilisée, elle donne une impression de sérénité qui n’est pas sans relation avec sa simplicité.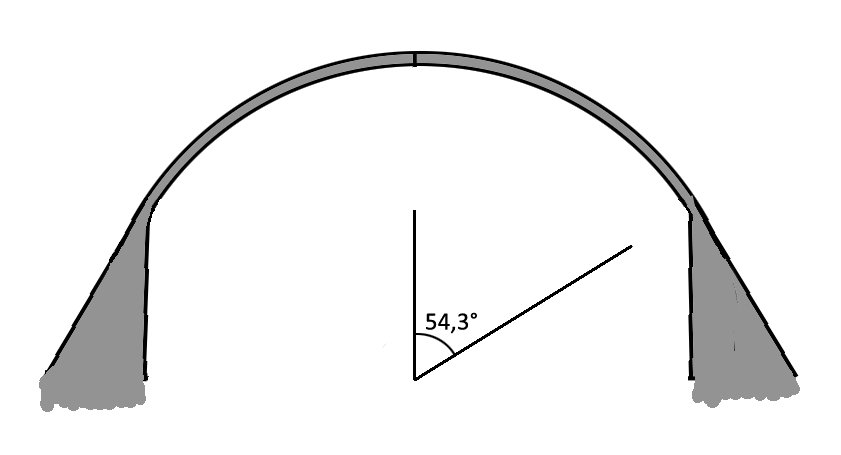
Si on part du sommet, pour une coupole sphérique de densité constante, les parallèles des premières calottes sont comprimées, 
plus on descend moins la compression est forte et à partir d’un certain angle depuis le sommet les parallèles sont tendus, autrement dit la coupole peut fissurer. On trouve que cet angle est de 54,3°.
C’est l’angle α tel que α=sin2α. Si on arrête une calotte sphérique à cette hauteur, elle est en compression et elle peut reposer sur un support qui ne reprend que les forces centrifuges, sans aucune solidarité horizontale, par exemple une série de murets dont les plans passent par l’axe de la coupole.
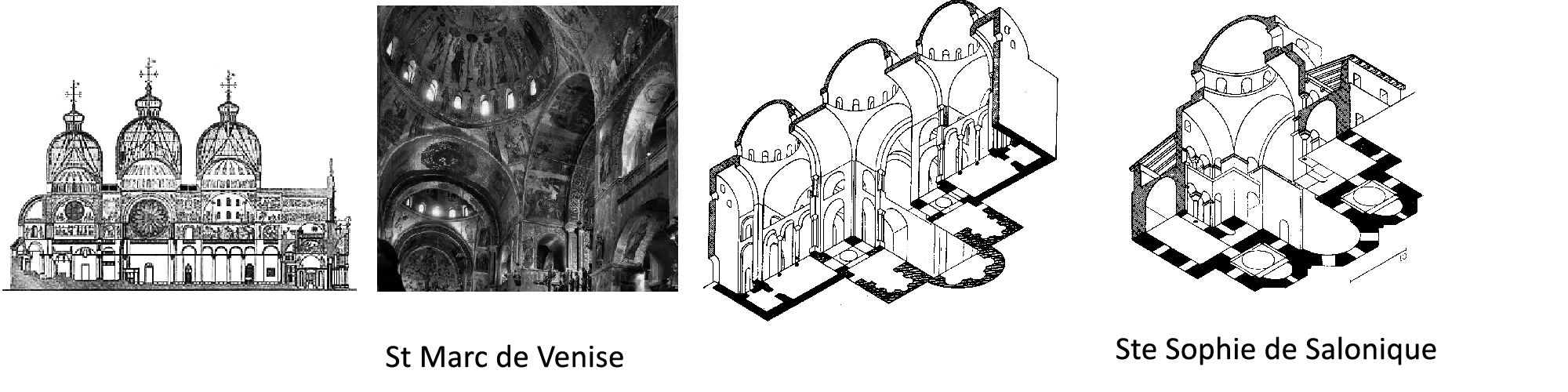
Un grand nombre de dômes, dans l’art d’Occident du Moyen-Âge, (cf. Focillon, Choisy) étaient constitués d’une calotte sphérique arrêtée à peu près à cette valeur de 54,3° et posée sur une couronne de fenêtres comme la principale coupole de Ste Sophie. Etait-ce à Ste Sophie la première fois que cette configuration était osée ? Etait-ce calculé ? Henri Focillon et Nikolaus Pevsner considèrent que Ste Sophie (et l’église des Saints Apôtres aujourd’hui disparue) eurent une influence majeure sur tout l’art d’Occident.
Les coupoles romaines — comme celle du Panthéon, ou celle du temple de Vesta dont il ne reste que trois colonnes mais que Palladio a dessinée — semblent partir de la même idée avec une solution différente : comme à partir de 54,3° la calotte sphérique a tendance à se fissurer, on assure la cohérence en chargeant davantage extérieurement à la sphère à partir de ce niveau. D’où ces sortes de cercles en escalier typiques.
Le panthéon de Rome et le temple de Vesta d’après Palladio
Ajoutons quelques remarques, d’abord que si Ste Sophie de Constantinople due être plusieurs fois réparée et renforcée c’est qu’elle subit depuis le 6e siècle pas moins de 16 séismes qui l’endommagèrent parfois gravement, d’autre part que St Pierre de Rome dont la coupole est quasi hémisphérique pour sa forme interne, ne doit sa sauvegarde qu’à des renforts rajoutés au 18e siècle au vu de graves fissures et après expertise de « mathématiciens » (Cf. P. Dubourg Glatigny et P. Le Blanc « Architecture et expertise mathématique » MEFRIM, t17, 189-218, 2005), et enfin que nous n’avons pas tenu compte de la présence d’un lanternon éventuel ce qui serait aisé dans l’esprit de ce que nous avons esquissé.